Sebelum mengambarkan identitas trigonometri, terlebih dahulu harus paham dengan trigonometri dasar yaitu sinus (sin), cosinus (cos), tangen (tan), cosecan (csc), secan (sec), dan cotangen (cot). Untuk itu, silahkan simak gambar di bawah ini.
 |
| Segitiga siku-siku |
Dari gambar segitiga siku-siku ABC di atas maka didapatkan bahwa:
Sin α = a/b
Cos α = c/b
Tan α = a/c
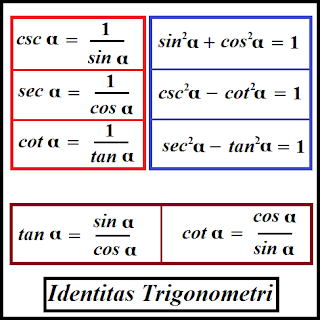
Csc α = b/a
Sec α = b/c
Cot α = c/a
Dari tan α, csc α, sec α, dan cot α akan didapatkan bentuk lain yakni:
Tan α = a/c
Tan α = (a/b)/(c/b)
Tan α = sin α/cos α
Csc α = b/a
Csc α = 1/(a/b)
Csc α = 1/sin α
Sec α = b/c
Sec α = 1/(c/b)
Sec α = 1/cos α
Cot α = c/a
Cot α = 1/( a/c)
Cot α = 1/tan α
Sekarang kita buktikan bahwa sin2 α + cos2 α = 1 dengan memakai teorema pythagoras yakni:
b2 = a2 + c2
b2 = a2 + c2
(a/sin α)2 = (b.sin α)2 + (b.cos α)2
a2/sin2 α = b2.sin2 α + b2.cos2 α
a2/sin2 α = b2(sin2 α + cos2 α)
a2/ b2sin2 α = sin2 α + cos2 α
a2/a2 = sin2 α + cos2 α
1 = sin2 α + cos2 α (terbukti)
Dengan memakai persamaan trigonometri dasar diatas maka persamaan identitas trigonometri sin2 α + cos2 α = 1 sanggup dibuktikan sebagai berikut.
sin2 α + cos2 α = 1
(a/b)2 + (c/b)2 = 1
a2/b2 + c2/b2 = 1
(a2 + c2)/b2 = 1
b2/b2 = 1
1 = 1 (terbukti)
Dari persamaan identitas trigonometri sin2 α + cos2 α = 1 akan didapatkan bentuk identitas lain yaitu sebegai berikut.
Jika sama-sama dibagi dengan sin2 α maka akan didapatkan:
sin2 α + cos2 α = 1
sin2 α/sin2 α + cos2 α/sin2 α = 1/sin2 α
1 + cot2 α = csc2 α
csc2 α – cot2 α = 1
Sedangkan, bila sama-sama dibagi dengan cos2 α maka akan didapatkan:
sin2 α + cos2 α = 1
sin2 α/cos2 α + cos2 α/cos2 α = 1/cos2 α
tan2 α + 1 = sec2 α
sec2 α – tan2 α = 1
Note: Identitas csc α, sec α dan cot α (dalam kotak warna merah) disebut sebagai identitas kebalikan. Identitas selanjutnya (dalam kotak berwarna biru) disebut sebagai identitas Pythagoras. Sedangkan identitas terakhir, tan α dan cot α (dalam kotak warna cokelat) disebut sebagai identitas rasio.