photo lineviral_1.png

Best Online Stock Trading Brokers for 2018 If you’re looking for a way to build more wealth in 2018, getting started with one of the best online brokerage accounts is a solid first step. Doing so will allow you to invest outside your traditional retirement accounts and on your own terms. The best part is, the best online brokerage firms charge little or no fees and offer excellent resources that can help you learn more about investing along the way. Of course, not all brokerage firms are created equal, and that’s why we took the time to break down each of their details and rank the top options on an array of factors. If you’re looking for a new way to invest this year and are ready to strike out on your own, the following online brokerage accounts should be at the top of your list.What Matters When You Trade Stocks on Your Own? Managing your own money can be a stressful endeavor. To minimize this, and to minimize information overload that tends to come from watching the markets 24/7, there are a few must-haves to look for in an online broker. Clean interface. When I trade, I want to be able to easily find my order entry ticket. I don’t want it buried under a number of drop downs. This interface should have intuitive access to see your balance, available cash, positions with real time P/L and all be easily navigated. Quick access to basic charting. A chart tells me where the stock has been recently. I don’t trade minute to minute anymore, so I don’t need complex tools like stochastics or retracement lines. All that’s important is that I have a basic chart on a yearly, monthly, weekly, daily and intra day time period. I use a chart to see current price relative to those time periods, mainly to avoid purchasing at a bad price. Low fees. One of the biggest roadblocks to building wealth is fees incurred to invest your hard-earned dollars. Because the fees charged by different brokerage firms vary so dramatically, it’s crucial to seek out options that charge low fees (or no fees) for account management and trades. There are over 50 online brokerages where you can open an account. Beyond the my three rules above, best online brokerage accounts aren’t just for trading stocks. Sure, many of them started as online stock trading accounts, but now they’re full-fledged trading, saving, investing, retirement planning, and banking machines. This industry is more complex than the average person thinks. You shouldn’t just pick any online broker and sign up for an account. The best online broker for one person is often completely different for the next person. Use this resource as a guide to your decision process. Figure out what features are best for you, and make your selection. What Makes a Great Online Broker? I analyzed a number of elements to come to my decision on which brokers are the best. Later in this post, I provide full details on how I selected the best online brokerages. When you take all the features, resources, trading platforms, and technology into account (while also considering every type of trader), the full-service brokers, like E*TRADE and TD Ameritrade are the best for the largest number of people. For those simply looking to make cheap trades, I would recommend going with Optionshouse. If you’re a very advanced trader, high-volume trader, or a professional who manages money, I recommend going with Interactive Brokers. However, I didn’t include Interactive Brokers on my list because they’re best for a very small group of traders and the platform is very complex. Top Qualities of Standout Online Trading Platforms Quality trading tools and technology Multiple trading platforms for all levels of traders Excellent mobile trading features Solid navigation that displays the relevant information where you want it Quality educational resources and research for trader development There’s more to selecting an online broker than price. You have to consider the resources you’re getting for the cost you pay per trade. For example, my colleague, who is also an ex-trader, likes to use a combination of stock and options trade in his longer-term trading. He recently switched over to Fidelity because he really liked the cash management features, but was very disappointed by complex order entry, sub-par options execution and frustrating navigation. He’s currently making the switch to one of the brokers I profile here.
Best Online Stock Trading Brokers for 2018 If you’re looking for a way to build more wealth in 2018, getting started with one of the best online brokerage accounts is a solid first step. Doing so will allow you to invest outside your traditional retirement accounts and on your own terms. The best part is, the best online brokerage firms charge little or no fees and offer excellent resources that can help you learn more about investing along the way. Of course, not all brokerage firms are created equal, and that’s why we took the time to break down each of their details and rank the top options on an array of factors. If you’re looking for a new way to invest this year and are ready to strike out on your own, the following online brokerage accounts should be at the top of your list.What Matters When You Trade Stocks on Your Own? Managing your own money can be a stressful endeavor. To minimize this, and to minimize information overload that tends to come from watching the markets 24/7, there are a few must-haves to look for in an online broker. Clean interface. When I trade, I want to be able to easily find my order entry ticket. I don’t want it buried under a number of drop downs. This interface should have intuitive access to see your balance, available cash, positions with real time P/L and all be easily navigated. Quick access to basic charting. A chart tells me where the stock has been recently. I don’t trade minute to minute anymore, so I don’t need complex tools like stochastics or retracement lines. All that’s important is that I have a basic chart on a yearly, monthly, weekly, daily and intra day time period. I use a chart to see current price relative to those time periods, mainly to avoid purchasing at a bad price. Low fees. One of the biggest roadblocks to building wealth is fees incurred to invest your hard-earned dollars. Because the fees charged by different brokerage firms vary so dramatically, it’s crucial to seek out options that charge low fees (or no fees) for account management and trades. There are over 50 online brokerages where you can open an account. Beyond the my three rules above, best online brokerage accounts aren’t just for trading stocks. Sure, many of them started as online stock trading accounts, but now they’re full-fledged trading, saving, investing, retirement planning, and banking machines. This industry is more complex than the average person thinks. You shouldn’t just pick any online broker and sign up for an account. The best online broker for one person is often completely different for the next person. Use this resource as a guide to your decision process. Figure out what features are best for you, and make your selection. What Makes a Great Online Broker? I analyzed a number of elements to come to my decision on which brokers are the best. Later in this post, I provide full details on how I selected the best online brokerages. When you take all the features, resources, trading platforms, and technology into account (while also considering every type of trader), the full-service brokers, like E*TRADE and TD Ameritrade are the best for the largest number of people. For those simply looking to make cheap trades, I would recommend going with Optionshouse. If you’re a very advanced trader, high-volume trader, or a professional who manages money, I recommend going with Interactive Brokers. However, I didn’t include Interactive Brokers on my list because they’re best for a very small group of traders and the platform is very complex. Top Qualities of Standout Online Trading Platforms Quality trading tools and technology Multiple trading platforms for all levels of traders Excellent mobile trading features Solid navigation that displays the relevant information where you want it Quality educational resources and research for trader development There’s more to selecting an online broker than price. You have to consider the resources you’re getting for the cost you pay per trade. For example, my colleague, who is also an ex-trader, likes to use a combination of stock and options trade in his longer-term trading. He recently switched over to Fidelity because he really liked the cash management features, but was very disappointed by complex order entry, sub-par options execution and frustrating navigation. He’s currently making the switch to one of the brokers I profile here.
» » Contoh Soal Dan Pembahasan Menghitung Jarak Titik Ke Garis Pada Kubus

Contoh Soal Dan Pembahasan Menghitung Jarak Titik Ke Garis Pada Kubus

Agar lebih gampang memahami rujukan soal di bawah ini, alangkah baiknya bila anda sudah memahami cara menghitung jarak titik ke garis yang sudah dibahas pada postingan sebelumnya (silahkan baca: cara menghitung jarak titik ke titik, garis, dan bidang). Jika sudah paham dengan materinya, silahkan simak dan pahami rujukan soal di bawah ini.

Contoh Soal 1
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6√3 cm. Titik P terletak pada garis AB dengan jarak B ke P yaitu 6 cm. Tentukan jarak titik B ke garis PC.

Penyelesaian:
Untuk memudahkan menuntaskan soal ini kita gambar dulu bentuk kubusnya, menyerupai gambar di bawah ini.
Agar lebih gampang memahami rujukan soal di bawah ini Contoh Soal dan Pembahasan Menghitung Jarak Titik ke Garis Pada Kubus

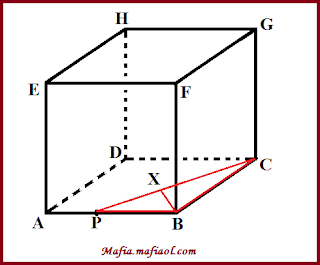
Dari gambar di atas maka akan didapatkan sebuah berdiri datar segitiga siku-siku, di mana titik siku-sikunya berada di B. Titik X berada di garis PC dan BX merupakan garis tinggi segitiga BCP dimana garis PC tegak lurus dengan garis BX. Pertama, cari panjang PC dengan teorema phytagoras yakni:
PC2 = BP2 + BC2
PC2 = 62 + (6√3)2
PC2 = 36 + 108
PC2 = 144
PC = √144
PC = 12 cm

Jarak titik B ke garis PC sama dengan jarak BX yang sanggup dicari dengan memakai rumus luas segitiga yakni:
LΔ = ½ PB × BC
dan
LΔ = ½ PC × BX
maka:
½ PB × BC = ½ PC × BX
PB × BC = PC × BX
6 × 6√3 = 12 × BX
6√3 = 2 × BX
BX = 3√3
Jadi, jarak titik B ke garis PC yaitu 3√3 cm

Contoh Soal 2
Diketahui kubus ABCD.EFGH dengan panjang rusuk 5√2 cm. Titik P terletak pada garis AE dengan 3PA = 2PE. Tentukan jarak titik P ke diagonal FH.

Penyelesaian:
Kita gambar dulu bentuk kubusnya, maka akan tampak menyerupai gambar di bawah ini:
Agar lebih gampang memahami rujukan soal di bawah ini Contoh Soal dan Pembahasan Menghitung Jarak Titik ke Garis Pada Kubus
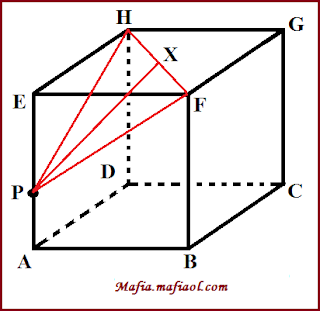
Jika 3PA = 2PE, maka:
PA : PE = 2 : 3, akibatnya:
AE : PE = 5 : 3
PE = 3AE/5
PE = 3×5√2/5
PE = 3√2

PH2 = PE2 + EH2
PH2 = (3√2)2 + (5√2)2
PH2 = 18 + 50
PH2 = 68
PH = 2√17

HF2 = EF2 + EH2
HF2 = (5√2)2 + (5√2)2
HF = 10 cm

FX = ½ HF
FX = ½ × 10
FX = 5
Jika titik P, F, dan H dihubungkan maka akan terbentuk segitiga sama kaki menyerupai gambar di bawah ini.
Agar lebih gampang memahami rujukan soal di bawah ini Contoh Soal dan Pembahasan Menghitung Jarak Titik ke Garis Pada Kubus

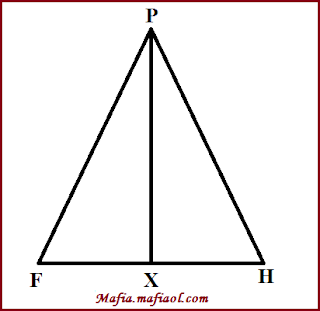
Maka:
PX2 = PH2 – FX2
PX2 = (2√17)2 – 52
PX2 = 68 – 25
PX = √43 cm
Jadi, jarak titik P ke diagonal FH yaitu √43 cm

Nah demikian rujukan soal dan pembahasan menghitung jarak titik ke garis pada berdiri ruang kubus, bila ada permasalahan atau hambatan dalam memahami rujukan soal ini, silahkan tanyakan pada kolom kometar. Kita niscaya bisa.
Share on Facebook
Share on Twitter
Share on Google+
Share on LinkedIn
close