Agar lebih gampang menguasai konsep hukum cosinus pada segitiga terlebih dahulu harus paham dengan perbandingan trigonometri pada suatu segitiga siku-siku khususnya definisi sinus dan cosinus suatu sudut. Oke pribadi saja ke pembahasan. Silahkan simak gambar di bawah ini.
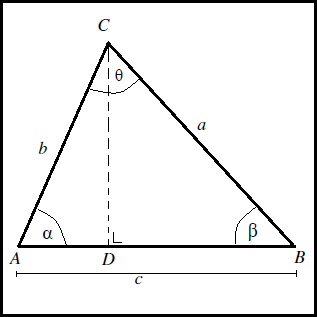
Dari gambar segitiga sebarang ABC di atas ditarik sebuah garis dari titik C menuju gari AB yang tegak lurus sehingga membentuk garis tinggi pada segitiga ABC. Di mana ÐCAB = α, ÐABC = β, ÐBCA = θ, AC = b, AB = c dan BC = a.
Sekarang perhatikan ΔADC, dengan memakai definisi sinus maka kita akan dapatkan panjang CD adalah:
sin α = CD/AC
CD = AC.sin α
CD = b.sin α (persamaan I)
Sedangkan panjang AD sanggup dicari dengan memakai definisi cosinus yakni:
cos α = AD/AC
AD = AC.cos α
AD = b.cos α (persamaan II)
Sekarang perhatikan ΔBCD, dengan menggunakan teorema pythagoras, dengan mensubtitusikan persamaan I dan II akan diperoleh:
BC2 = BD2 + CD2
BC2 = (AB – AD)2 + CD2
BC2 = AB2 –2AB.AD + AD2 + CD2
BC2 = AB2 –2AB. b.cos α + (b.cos α)2 + (b.sin α)2
BC2 = AB2 –2AB.b.cos α + b2.cos2 α + b2.sin2 α
a2 = c2 – 2bc.cos α + b2.cos2 α + b2.sin2 α
a2 = c2 – 2bc.cos α + b2.(cos2 α + sin2 α)
ingat identitas trigonometri bahwa cos2 α + sin2 α = 1, maka persamaannya menjadi:
a2 = c2 – 2bc.cos α + b2
a2 = b2 + c2 – 2bc.cos α
Dengan cara yang sama kita juga sanggup melaksanakan langkah untuk sudut β dan θ. Makara sanggup disimpulkan bahwa setiap segitiga ABC dengan panjang sisi- sisi berturut-turut yakni a, b dan c satuan panjang dan besar sudut di hadapan sisi-sisi berturut-turut yakni α, β, dan θ (seperti pada gambar ΔABC di atas) maka berlaku hukum cosinus berikut:
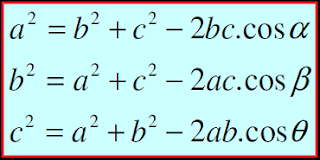
Untuk memantapkan pemahaman Anda perihal hukum cosinus pada segitiga silahkan simak pola soal di bawah ini.
Contoh Soal 1
Diketahui segitiga ABC, dengan panjang AB = 5 cm, BC = 7 cm dan sudut B = 60°, tentukan panjang sisi AC.
Penyelesaian:
Jika digambarkan segitiganya maka akan tampak menyerupai gambar di bawah ini.
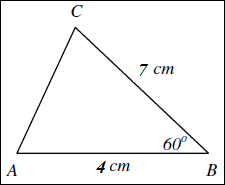
Dengan memakai hukum cosinus maka kita akan sanggup mencari sisi-sisi pada segitiga tersebut yakni:
AC2 = AB2 + BC2 – 2AB.BC.cos 60°
AC2 = 42 + 72 – 2.4.7. ½
AC2 = 16 + 49 – 28
AC2 = 37
AC = √37 cm
Contoh Soal 2
Diketahui segitiga ABC, dengan panjang AB = 9 cm, AC = 7 cm, dan BC = 8 cm. Tentukan nilai sin B.
Penyelesaian:
Jika digambarkan segitiganya maka akan tampak menyerupai gambar di bawah ini.
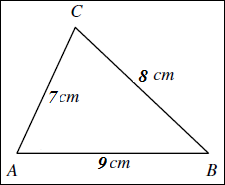
Dengan memakai hukum cosinus maka kita cari dulu nilai cos β yakni:
AC2 = AB2 + BC2 – 2AB.BC.cos B
72 = 92 + 82 – 2.9.8. cos B
49 = 81 + 64 – 144.cos B
96 = 144.cos B
cos B = 96/144
cos B = 2/3
cos B = x/r
maka:
r2 = x2 + y2
32 = 22 + y2
y2 = 5
y = √5
sehingga nilai sin B = y/r = √5/3
Cara lain, dengan memakai identitas trigonometri bahwa cos2 B + sin2 B = 1 maka:
sin2 B = 1 – cos2 B
sin2 B = 1 – (2/3)2
sin2 B = 1 – 4/9
sin2 B = 9/9 – 4/9
sin2 B = 5/9
sin B = √(5/9)
sin B = √5/3
Soal Tatangan
Sebuah bundar yang di dalam terdapat segiempat tali busur menyerupai gambar di bawah ini.
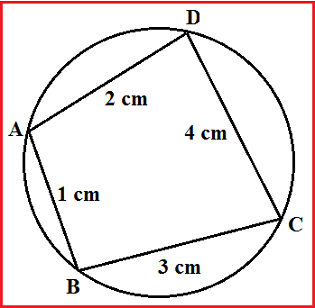
Panjang tali busur AB = 1 cm, BC = 3 cm, CD = 4 cm dan AD = 2 cm. Tentukan nilai sin A

