Postingan sebelumnya sudah membahas ihwal penerapan gaya sentripetal pada sebuah benda yang diputar secara vertikal. Dalam bahan tersebut sudah dijelaskan bagaimana memilih besarnya gaya tegangan tali pada dikala benda yang diputar berada pada posisi horizontal (tegangan tali tegak lurus dengan gaya berat), titik terendah dan titik tertinggi. Gaya tegangan tali bernilai maksimum apabila benda berada di titik terendah (paling bawah), dan bernilai minimum pada dikala benda berada di titik tertinggi (paling atas).
Pada kesempatan kali ini masih membahas ihwal benda yang diputar secara vertikal. Bahasan kali ini akan mengulas ihwal kecepatan minimum pada titik tertinggi dan titik terendah sebuah benda bila diputar secara vertikal semoga benda tersebut tidak terpental (keluar) meninggalkan lintasan.
Oke kita pribadi saja, kini coba perhatikan gambar di bawah ini.
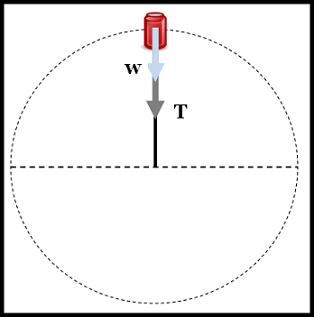
Gambar di atas merupakan sebuah kaleng diikat dengan tali kemudian diputar secara vertikal. Pada titik tertinggi gaya berat dan tegangan tali akan secara tolong-menolong menuju ke bawah atau sentra lingkaran.
Agar benda sanggup melaksanakan gerak melingkar, kecepatan minimal ketika berada di titik tertinggi diperoleh dengan syarat gaya normal nol (gaya normal diwakili oleh gaya tegangan tali), sehingga berlaku:
Fs = ΣF
Fs = T + w
mv2/R = mg
v2/R = g
v2 = Rg
v = √Rg
Sedangkan kecepatan minimum untuk titik terendah sanggup ditentukan dengan memakai aturan kekekalan energi. Hukum kekekalan energi menyatakan bahwa energi tidak sanggup diciptakan maupun dimusnahkan, melainkan sanggup berubah bentuk ke bentuk yang lain. Dalam hal ini, pada gerak melingkar secara vertikal, energi mekanik pada titik tertinggi sama dengan energi mekanik pada titik terendah. Energi mekanik ialah energi yang dimiliki oleh suatu benda alasannya ialah gerakannya atau posisinya yakni energi kinetik (Ek) atau energi potensial (Ep). Sekarang perhatikan gambar di bawah ini.

Pada gambar di atas sebuah kaleng diputar secara vertikal dari titik A menuju titik B, maka:
Energi mekaik A = Energi mekanik B
Ep A + Ek A = Ep B + Ek B
mgh + ½ mvA² = ½ m vB² + 0
Ingat h = 2R, maka:
mg2R + ½mvA² = ½mvB²
2gR + ½vA² = ½vB²
Ingat kecepatan minimun di titik tertinggi (titik A) ialah v = √gR, maka:
2gR + ½(√gR)² = ½vB²
2gR + ½gR = ½vB²
5gR = vB²
vB = √5gR
Jadi kecepatan minimum di titik terendah sanggup memakai persamaan:
v = √5gR
Kecepatan minimum ini berlaku bila benda bergerak di dalam bulat contohnya dikala roll coaster bergerak melingkar dimana posisi roll coaster terbalik, menyerupai gambar di bawah ini.

Sedangkan bila benda bergerak di luar lingkaran, contohnya sebuah kendaraan beroda empat bergerak di jalan yang melengkung, maka kecepatan minimum ini akan menjadi kecepatan maksimum. Untuk memantapkan pemahaman kau ihwal kecepatan minimum dan maksimum pada benda yang berputar atau bergerak melingkar secara vertikal, silahkan simak pola soal d bawah ini.
Contoh Soal 1
Seorang anak memasukan air ke dalam ember, kemudian diputar secara melingkar dengan tali yang panjangnya 0,9 m secara vertikal. Tentukan kecepatan minimum di titik tertinggi dan terendah bejana yang diputar semoga air yang ada di dalamnya tidak tumpah.
Penyelesaian:
R = 0,9 m
g = 10 m/s2
Kecepatan di titik tertinggi sanggup memakai persamaan:
v = √Rg
v = √(0,9 m)(10 m/s2)
v = 3 m/s
Sedangkan kecepatan di titik terendah sanggup memakai persamaan:
v = √5gR
v = √(5)(0,9 m)(10 m/s2)
v = 3√5 m/s
Contoh Soal 2
Agar menjadi lebih besar lengan berkuasa sebuah jembatan dibangun melengkung ke atas (titik sentra di bawah jembatan) dengan jari-jari 90 m. Sebuah kendaraan beroda empat bermassa 500 kg melintas
di atas jembatan dengan kecepatan 72 km/jam. Berapakah kecepatan maksimum yang diperbolehkan dikala melewati jembatan dan apakah kendaraan beroda empat tersebut bergerak dengan kondusif dengan kecepatan tersebut di atas?
Penyelesaian:
R = 90 m
m = 500 kg
v = 72 km/jam = 20 m/s
g = 10 m/s2
Kecepatan maksimum yang diperbolehkan dikala melewati jembatan yakni:
v = √gR
v = √(90 m)(10 m/s2)
v = 30 m/s
Karena kendaraan beroda empat bergerak dengan kecepatan 20 m/s sedangkan kecepatan maksimum 30 m/s, maka kendaraan beroda empat tersebut bergerak masih dalam keadaan kondusif bila melewati jembatan tersebut.
Demikian pembahasan kecepatan minimum pada benda yang diputar secara vertikal. Mohon maaf bila ada kata atau perhitungan yang salah dalam postingan ini. Jika ada permasalahan dalam memahami bahan ini silahkan tanyakan pada kolom komentar. Kita niscaya bisa.

