Contoh dalam kehidupan sehari-hari yang menerapkan gaya sentripetal pada benda yang diputar secara vertikal yakni permainan atau wahana bianglala dan roller coaster. Kedua permainan ini sanggup kita jumpai di daerah bermain Dunia Fantasi (Dufan) Jakarta.
 |
| Wahana Bianglala. Sumber: Flickr |
Selain kedua pola di atas, penerapan gaya sentripetal pada benda yang diputar secara vertikal sanggup kita contohkan pada ketika kita memutar-mutar sebuah kaleng bekas dengan seutas tali.
Berbeda dengan benda yang diputar secara horizontal dimana gaya berat tidak ikut berpengaruh, tetapi jikalau sebuah benda diputar secara vertikal maka gaya berat benda besar lengan berkuasa dalam penerapan gaya sentripetal kecuali pada posisi horizontal saja. Di setiap titik lintasan gaya tegangan tali sanggup ditentukan besarnya. Gaya tegangan tali bernilai maksimum apabila benda berada di titik terendah (paling bawah), dan bernilai minimum pada ketika benda berada di titik tertinggi (paling atas).
Pada ketika gaya berat (w) tegak lurus gaya tegangan tali (T) gaya sentripetal berupa gaya tegangan tali alasannya yakni gaya berat tidak mempunyai proyeksi terhadap arah mendatar, menyerupai gambar berikut ini.
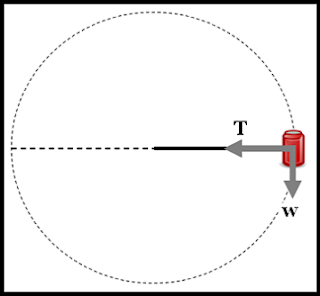 |
| Posisi kaleng horizontal dengan tali pada ketika diputar vertikal |
Fenomena menyerupai ini menyerupai dengan penerapan gaya sentripetal pada benda yang diputar secara horizontal dan persamaannya pun sama (gaya sentripetal berupa gaya tegangan tali) yakni:
Fs = T
mv2/R = T
v2 = RT/m
Untuk lebih jelasnya silahkan baca postingan sebelumnya wacana penerapan gaya sentripetal pada benda yang diputar horizontal.
Apabila posisi benda berada di titik tertinggi (paling atas) lintasan menyerupai ditunjukkan gambar berikut ini.
 |
| Posisi kaleng di titik tertinggi pada ketika diputar vertikal |
Gaya berat dan tegangan tali akan sama-sama menuju sentra lingkaran, maka persamaan gaya sentripetal akan menjadi sebagai berikut.
Fs = ΣF
Fs = T + w
mv2/R = T + mg
T = mv2/R – mg
T = m(v2/R – g)
Sedangkan apabila benda berada di titik terendah lintasan gaya berat akan berlawanan arah dengan gaya tegangan tali, menyerupai ditunjukan gambar berikut ini.
 |
| Posisi kaleng di titi terendah |
Persamaan gaya sentripetal akan menjadi sebagai berikut.
Fs = ΣF
Fs = T – w
mv2/R = T – mg
T = mv2/R + mg
T = m(v2/R + g)
Apabila benda berada di sembarang titik lainnya dalam lintasan melingkar dengan membentuk sudut α terhadap garis vertikal maka gaya berat harus diuraikan vektor gayanya, menyerupai gambar di bawah ini.
 |
| Posisi kaleng di titik tertentu |
Persamaan gaya sentripetal secara umum akan menjadi sebagai berikut.
Fs = ΣF
Fs = T – w cos α
mv2/R = T – mg cos α
T = mv2/R + mg cos α
T = m(v2/R + g cos α)
Bagaimana cara memilih kecepatan minimum dan maksimum pada ketika benda berada di titik tertinggi dan terendah? Akan dibahas pada postingan selanjutnya. Silahkan pahami terlebih dahulu pola soal di bawah ini.
Contoh Soal 1
Sebuah kaleng massanya 100 gr diikat dengan tali dan diputar sehingga lintasannya berbentuk bulat vertikal dengan jari-jari 0,5 m. Jika kecepatan sudut 6 rad/s dan g = 10 m/s2, maka tentukan tegangan tali pada arah horizontal, di titik terendah dan di titik tertinggi.
Penyelesaian:
m = 100 gr = 0,1 kg
R = 0,5 m
ω = 6 rad/s
g = 10 m/s2
Untuk tegangan tali arah horizontal sanggup memakai persamaan:
T = mv2/R
Ingat v = ωR, maka:
T = mω2R
T = (0,1 kg)(6 rad/s)2(0,5 m)
T = 1,8 N
Untuk tegangan tali di titik terendah sanggup memakai persamaan:
T = m(v2/R + g)
T = m(ω2R + g)
T = (0,1 kg)[(6 rad/s)2(0,5 m) + (10 m/s2)]
T = 2,8 N
Untuk tegangan tali di titik tertinggi sanggup memakai persamaan:
T = m(v2/R – g)
T = m(ω2R – g)
T = (0,1 kg)[(6 rad/s)2(0,5 m) – (10 m/s2)]
T = 0,8 N
Contoh Soal 2
Sebuah kaleng bekas dengan massa 200 gr diikat dengan tali dan diputar sehingga lintasannya berbentuk bulat vertikal dengan jari-jari 0,5 m. Jika kecepatan sudut kaleng 10 rad/s dan g = 10 m/s2, tentukan tegangan tali pada ketika kerikil membentuk sudut 60° terhadap jari-jari vertikal lintasan.
Penyelesaian:
m = 200 gr = 0,2 kg
R = 0,5 m
ω = 10 rad/s
g = 10 m/s2
α = 60°
Untuk memilih tegangan tali pada ketika kerikil membentuk sudut α terhadap jari-jari vertikal lintasan sanggup memakai persamaan:
T = m(v2/R + g cos α)
T = m(ω2R + g cos α)
T = (0,2 kg)[(10 rad/s)2(0,5 m) + (10 m/s2)(cos 60)]
T = (0,2 kg)[(10 rad/s)2(0,5 m) + (10 m/s2)(0,5)]
T = 11 N
Demikian pembahasan penerapan gaya sentripetal pada benda yang diputar secara vertikal. Mohon maaf jikalau ada kata atau perhitungan yang salah dalam postingan ini. Jika ada permasalahan dalam memahami bahan ini silahkan tanyakan pada kolom komentar. Kita niscaya bisa.

